You have likely heard the term “fine art” referring to a pursuit such as painting, sculpture, or poetry. But the notion of mathematics as art, let alone a fine art, may be positively alien and even offensive to some. How could the source of so much suffering in high school be art?
If you would be so inclined, allow me to entertain and explain such a radical proposition.
But firstly, what the hell do we mean by the phrase, “fine art”? Here, Mortimer Adler gives us somewhere to start. In his book,How To Think About the Great Ideas, Adler notes that the fine arts are first and foremost useless. By this, we do not mean that fine arts are valueless – this is an entirely different notion. Rather, a work which is not in the category of fine arts is,
…a thing which serves an end, a means which function toward some ulterior end or purpose. And there is no difficulty in understanding that a shoe or a house or a desk is a work of useful art that helps us in some particular connection in our action, or is practically useful. (How to Think About the Great Ideas, p240).
So let us not get caught up in the possibly derogatory connotations of the term “useless” – since that’s not what we mean here. Now that we cleared that up, we can outline some boundaries within mathematics itself that cannot be considered fine arts; namely, almost everything you learn in school. Calculus, rates of change, geometry, logarithms, and so on. It would be absurd to propose that computing derivatives, or doing arithmetic calculations is a fine art – indeed such a claim would be equivalent to saying that mixing paint is in the same category as a painting itself. Calculus, like mixing paint, is a necessary process which the mathematician must be proficient at – both for practicality and to bring beauty into the world, through pure mathematics.
Now here we depart into the area of pure mathematics, which is my current, central focus of study at university. For almost all reading this, that title – pure mathematics – may not mean much. It may evoke ideas of abstraction, esoteric academia, and perhaps an associated sense of entitlement to whomever dare say such a phrase. Does not the word “pure” imply there is something “impure” about other aspects of mathematics? Moreover, we do not say “pure physics”, or “pure biology”. By “pure”, do we not mean the kinds of math that the impure, filthy layman could never hope to understand, let alone actively practice?
On the contrary, I would hazard to defend the term, since it distinguishes the core precept of what mathematics is all about, from whatever it is that most students learn in school – rote memorization, computation, formula. These ideas are not mathematics. These are barely even the building blocks. They are merely the chaff, which without we could not distinguish nor appreciate the wheat.
Hopefully I haven’t lost you yet. If you’re still hanging in there, let me now do my best to describe what comes to my mind when I think of the phrase, pure mathematics:
Patterns.
Harmony expressed through symbols.
Coherent, overarching abstraction.
Language which describes the fabric of the universe.
Clever arguments. Theorems and proofs.
Undeniable truth.
Frustration, grit, confusion, blood sweat and tears.
I wish I could share directly what all that these words mean to me. As the last line above implies however, such a pursuit is not free of intellectual pain. If there is anything the layman could relate to the mathematician with, it is the feeling of utter frustration. There is simply no other subject which requires the artisan to allow themselves to be fully, and completely confused. I make a particular point of this because I believe it is in fact, integral (heh) to the art itself.
Pure mathematics is fundamentally, the study of abstract patterns understood through symbols. Very rarely might one come across a number like the comfortable “1’s”, “2’s” and “3’s”. Numbers aren’t even the tip of the iceberg. Imagine taking the idea of numbers itself, and abstracting it into some “mathematical object”. Now let that abstract object itself be our variable, X. Now let X contain elements which satisfy certain axioms, like addition and multiplication – but never-mind what it actually is that we are adding or multiplying – for it may very well be that they are numbers, polynomials, or something else entirely. It doesn’t matter, because what the pure mathematician cares about is the abstraction, and the rules the abstraction abides by. Now finally, we build a theory around the idea of “X”, with names like rings, groups, quotients, idempotents, nilpotents, domains, modules, and so on.
Still with me?
That’s a shitty overview of the field of mathematics known as Abstract Algebra – which is concerned with studying symmetries and properties inherent to the ideas of addition and multiplication. I appeal to such an example since, at the time of writing, I am taking a course in Algebraic Geometry, which studies sets of polynomial equations in arbitrary mathematical spaces. Great fun, quite difficult, but more importantly – absolutely enthralling.
The point of that digression, however, was to outline how abstraction makes the mind work really damn hard. If you were confused over the last few paragraphs, then I have paradoxically sinned properly as a writer – since this was my purpose. Point being that abstractions are intrinsically difficult to understand. Only through long hours, hard work and being utterly, totally confused for stretches of time, can one ever hope to begin to grasp pure mathematics.
Now you may ask, where is the art in such a pursuit?
I can only appeal to images, to make my point.


Some mathematics students may roll their eyes at these, whilst the layman may simply gawk in astonishment, but promptly forget they ever saw such images. These images are at worst, just pretty. But at best, they indicate a deep underlying beauty in the simplest facts about the way our universe works under the hood. My argument is that these kinds of mathematical visualizations, by virtue of their aesthetic appeal, imply that mathematics can be a fine art. There is nothing useful about such visualizations (save for the scarce occasion were it may inform further intuition for a mathematician, or point to a curious area of inquiry) – but they are beautiful in and of themselves. Just like a panting, or a sculpture. They serve no other purpose than to strike awe – but what a sublime purpose it is.
It’s unfortunate that for the most part, without any further mathematical training, most people will never see the elegance and art that is intrinsic to the subject without visualizations.
For example, mathematical proofs are an aspect of mathematics that can on one hand, be brutal, unforgiving, horrendous and downright ugly. On the other hand, proofs can appear to strike at the heart of a deep pattern and elegance intrinsic to the nature of the universe itself. The Fundamental Theorem of Calculus, and Fundamental Theorem of Algebra, spring to mind.
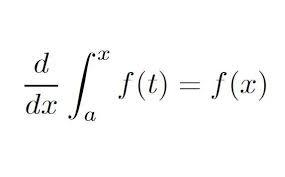
Sometimes the proof may be ugly, and the work to show it is true difficult and arduous, but the theorem itself state something of utter simplistic brilliance. Fermat’s Last Theorem, is perhaps the best example here.
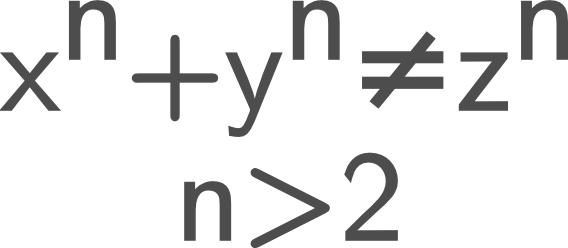
There is also the odd macroscopic nature of some proofs. Sometimes, a mathematician must use some crazy, infinitely sized mathematical object to prove a fact about finite things, as per the proof of Hilbert’s Basis theorem. Other times, we will use wild and fanciful tricks which seem more at home on the stage of a magician’s show. Mathematics is perhaps the only discipline in which one can go from totally and utterly depraved, confused and frustrated, to a state of blissful insight in a split second.
So, may we rightfully call pure mathematics a fine art? I think, for the most part, yes. But just as in the artistic pursuits, there are more and less aesthetically appealing objects, theorems and proofs in mathematics. Just as writing and painting can both be arduous and painful, so to is mathematics, before it bears the fruits of one’s labors. There is only one pronounced difference between this kind of art, and others – most of what you will see has already been discovered. Unlike the other fine arts, the objects of pure mathematics are vary rarely originally created by the mathematician – but this certainly doesn’t reduce the novelty and wonder of understanding a proof of a cool theorem for the first time for any one individual. In this manner, I think, pure mathematics is perhaps more personal of a fine art than any other – mathematical beauty is well and truly in the eye – or in most cases, mind – of the beholder. As a fine art, pure mathematics is often (but not always) useless. However, just as classical music is useless, we can also be sure in saying the world would be far less interesting without it.
-A
Leave a Reply